Codebox Software
Playing Blackjack with Machine Learning
Published:
Monte Carlo Reinforcement Learning is a simple but effective machine learning technique, that can be used to determine the optimal strategy for episodic games (i.e. games which are guaranteed to terminate). The learning process involves starting with some non-optimal strategy, such as picking moves at random, and then incrementally improving that strategy by playing multiple games, and making small changes to the strategy at the end of each one.
In order to be able to define a strategy, we need to identify all the various game 'states' that can exist. A state is a description of the current situation in the game, which contains all the details that we need to consider when deciding what to do, and no irrelevant information. For example, when playing a game of blackjack the state will need to contain information about what cards we have, and what card the dealer is showing.
A strategy consists of a set of rules that the player can use to decide what to do in each state, we can think of it as a long series of instructions of the form:
- In State 1 do Action A
- In State 2 do Action B
- In State 3 do Action A
- In State 4 do Action C
- ...
In blackjack the player is initially dealt 2 cards from the pack, and the dealer has a single card. One way to represent the initial state of the game would be to simply indicate what these 3 cards are, for example: "Player has A♠ and 3♦, Dealer has J♣". When playing with a single deck of 52 cards, this gives 52 x 51 x 50 = 132,600 possible starting states.
However we can reduce this number by discarding some irrelevant information. For example, the suit of the cards is ignored in blackjack, so we can remove this information from the state: "Player has A and 3, Dealer has J". The number of possible states is now much smaller: 13 * 13 * 13 = 2,197.
We can reduce the number of states in our example even further - in blackjack all face cards are treated as having a value of 10, and in general the individual card values do not matter, only the total value held by each player. The only exception to this rule is that Aces can have a value of either 1 or 11, so the state should indicate whether a player's hand contains an Ace or not.
In summary then:
- There are 10 possible Dealer states: 2,3,4,5,6,7,8,9,10,A
- There are 25 possible Player States:
- No Ace: 4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20
- With Ace: 13,14,15,16,17,18,19,20
- There are 10 x 25 = 250 total states
In order to develop a blackjack strategy using Monte Carlo Reinforcement Learning, we need to play many individual games. Each time we take an action we note which of our 250 states we were in, what action we took, and what the eventual outcome of the game was. A value called the 'return' can then be used to estimate how good/bad each action was. The return is calculated by deciding to what extent each of the individual actions that we took contributed to the eventual success or failure that occured at the end of the game. This calculation is performed using a discounting factor, which allocates more credit/blame to the later actions (which were closer to the point at which the result occurred) than to the earlier actions.
At first our actions are completely random, however because we are keeping a careful record of how much we won/lost by taking each action in each different state, as time goes on we can start to use this information to help pick the best action for the situation. One possible strategy would be to always select the action that has yielded the highest average return in the past, for example:
| State: | Player total = 8 with No Ace, Dealer total: 10 |
| Action = HIT | Action performed 4 times, total return = £20 |
| Action = STICK | Action performed 2 times, total return = £4 |
So the mean return for the action HIT is 20 ÷ 4 = £5 and for the action STICK it is 4 ÷ 2 = £2, so it seems like the best action to take in this situation is to HIT.
The problem with always picking the action with the highest return however, is that as soon as one action has started to deliver some positive returns we will continue picking that action forever, and never try any of the others - one of which might actually be better than the one we first tried.
A balance needs to be struck between exploration and exploitation. We want to try a variety of different actions, so that we have the opportunity to see which ones work and which ones do not, but we also want to exploit the profitable actions that we have already discovered. In order to achieve this balance we select the action with the highest mean return most of the time, but some proportion of the time we act randomly. This ensures that we will eventually explore all different actions, and be able to determine the best ones.
The frequency with which we should act randomly will vary according to the specifics of the game that we are playing, and experimentation is usually needed in order to determine the best value. As we continue to play the game, and our strategy becomes more reliable, we should gradually reduce the frequency with which random actions are taken, with this value approaching zero as we converge on the optimal strategy.
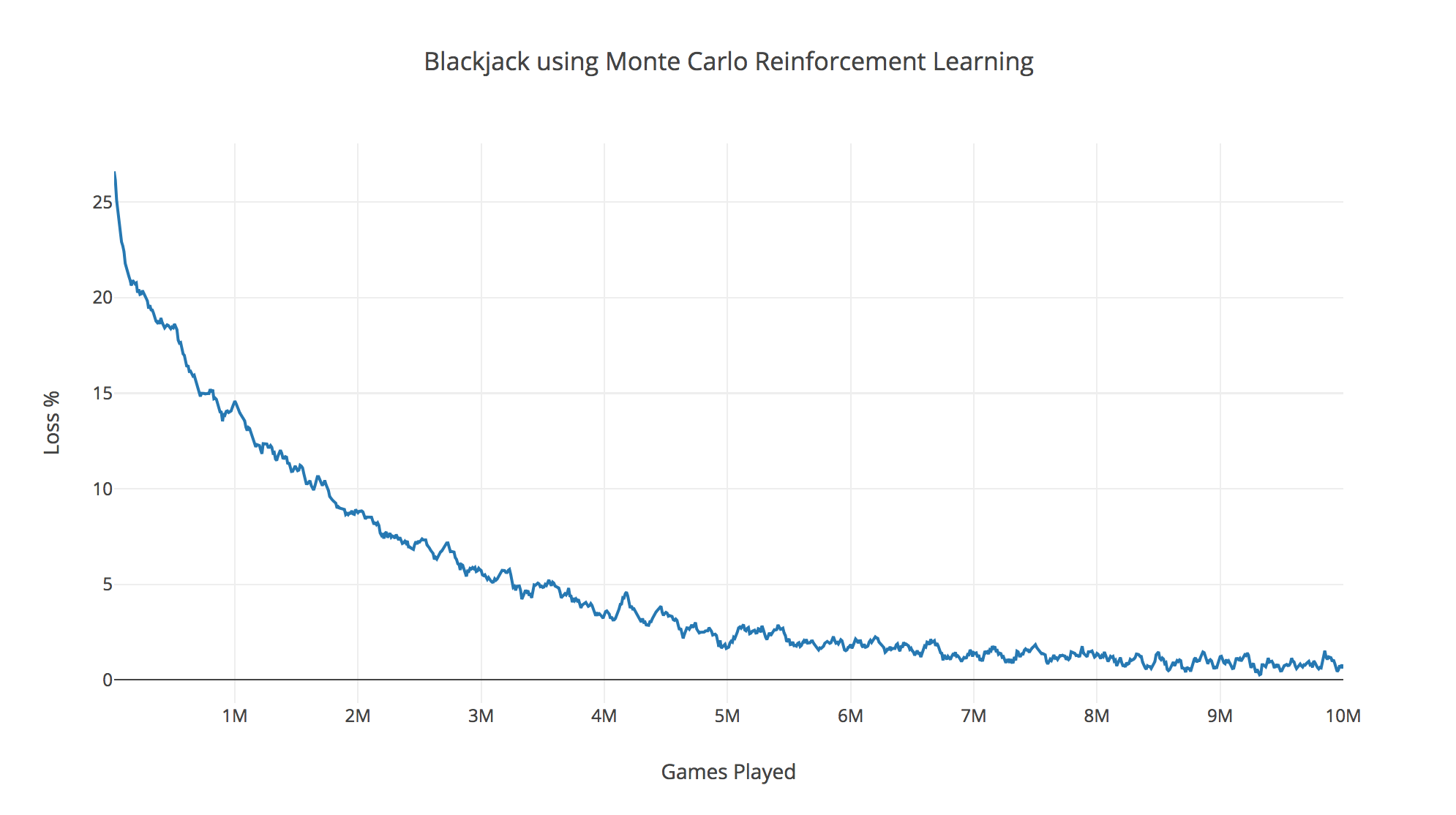
The graph below shows the results of applying this Monte Carlo strategy to the game of blackjack, played with a single deck of cards. The vertical axis indicates what proportion of the money that we wagered was lost. The horizontal axis shows how many games were played. Since the rules of blackjack always favour the dealer, it is not possible to actually make a profit in this game without counting cards, however a good strategy can reduce the dealer's edge to around 0.5%, which is roughly the level attained by our Reinforcement Learning agent in this experiment:
This video shows how the agent's strategy changed over the course of 5 million games. The coloured boxes indicate the action favoured
by the agent in each state.
- HIT - request another card from the dealer
- STK - do not request any more cards from the dealer
- DBL - double the current bet and draw one further card
- SUR - surrender, losing half the current bet and ending the game
We can see that the agent quickly learns to HIT when it has a low value hand, and to STICK when its hand is high. Its strategy becomes fairly stable after about 500,000 games, however small adjustments continue to be made to a few of the states right up until the end of the training period.